Hash functions have several applications in cryptography. In this article, you will learn the characteristics of hash functions and some of their applications. Also, I’ll describe some of the hash functions that are already being used. Lastly, you will learn about HMAC and an example of implementation.
Table of Contents
- Hash functions
- Cryptographic hash functions
- Cryptographic Hash functions applications
- Hash functions SHA-3
- HMAC
Hash functions
A hash function is a one-way function that transforms a message M into a message that will have a predefined length. One-way means that it is easy to compute given an input, but hard (or impossible) to invert given the image.
When we use a function to hash, anytime we apply the function to the same input, we will get the same output. The output is also known as a message digest.
A hash function is not an encryption mechanism. The reason behind this is that once we apply a hash function to a text, we won’t be able to obtain the original text from the hash result. This second part will be in an encryption mechanism the decryption of a text.
Cryptographic hash functions
We can divide hash functions into two groups: cryptographic hash functions and no cryptographic.
Although the two groups can generate a message digest, cryptographic hash functions must have the following security requirements.
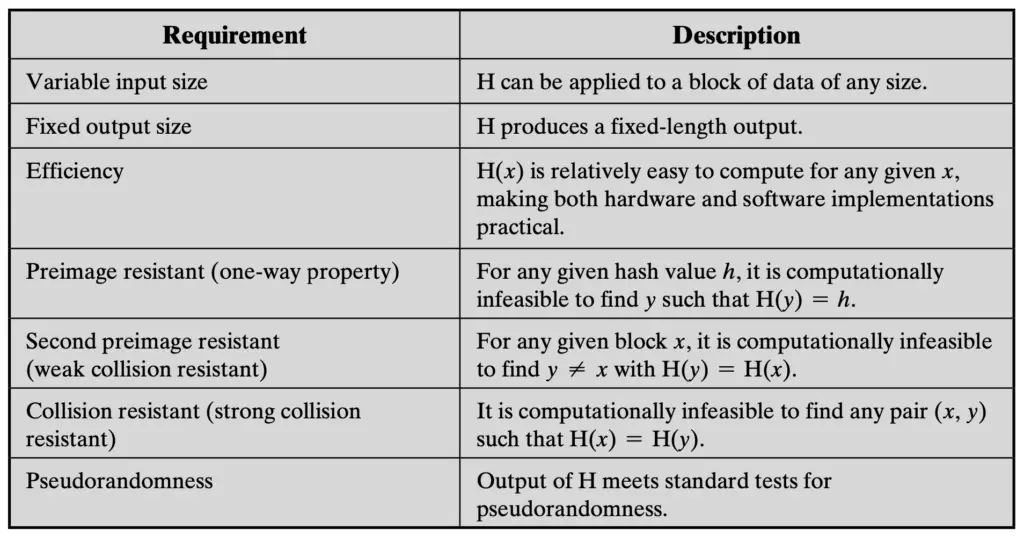
Preimage resistant: The preimage of a hash is the message we use as input to generate the hash (the message digest). Preimage resistance is that from the hash, it is computationally impossible to obtain the original message using the message digest. This is an important characteristic when we use hash functions to guarantee confidentiality. For instance, when we use it to store passwords. This requirement will guarantee that no one can see the password, even if it has the message digest. An important factor to considering when designing and implementing authentication mechanisms.
It is important to mention that the hash (the output of the hash function) has a fixed length. However, the input or message can have a variable length.
This fact shows us that there are more possible inputs than possible outputs. So, two inputs (messages) may have the same output (message digest). Therefore, we always must ensure that requirement off “Collision resistant”.
Notice that theoretically, you won’t eliminate the possibility of collisions. What you must guarantee is that it is computationally infeasible that a collision will occur.
Cryptographic Hash functions applications
If you examine the security requirements, you can understand that as a result, we can use hash functions to:
- store passwords: we cannot store passwords in plain text. If we do it then anyone with access to the computer (and the necessary permissions) can get your password from the place that is stored. But if we store the message digest (hash) then even if someone can get the digest, won’t be able to know the password because of the preimage resistant characteristic.
- digital signature: The digital signature process requires complex mathematical operations. Signing a large message is inefficient and takes a long time because of the complexity of the operations. That is why the best approach is to calculate a message digest (hash) from the message that we want to sign. Because the hash has a fixed length it is generally much smaller than the original message. Now we sign the message digest. Because the digest was created from the original message, signing the message digest is equivalent to sign the original message. If the original message is modified, the new message digest won’t match the signed message digest.
- Integrity: a way to check the integrity of a file is to publish the file’s hash. When someone downloads the file, you can calculate the hash of the downloaded file and compare it with the hash that was published. If the two hash are equals, then the downloaded file was properly downloaded.
- check a password before decrypting a message: when we design an encryption system, we can store the hash of the key that was used to encrypt the as part of the encrypted file. When the user types the key, it is compared to the hash to detect if it is correct before starting to decrypt and not try to decrypt the data with an incorrect key.
Hash functions SHA-3
The Secure Hash Algorithm (SHA) is considered a safe cryptographic function to use.
SHA-3 is the 3rd generation of the algorithm’s family preceded by SHA-1 and SHA-2. Each one has a set of hash functions in different versions.
SHA-3 groups 6 functions published by the National Institute of Standards and Technology (NIST) of the United States. Its characteristics are published in NIST.FIPS.202.
6 functions are made up of 4 hash functions and 2 extensible output functions (XOF).
Extensible output functions allow generating a hash of any length and it is possible to adapt it to different size requirements than those defined in the hash functions.
The final number of the hash function represents the length of the output. For example, SHA3-256 represents the SHA3 function with 256-bit output.
In the case of extensible output functions, the number represents the security level of that extensible output.
SHA-3 Hash functions
- SHA3-224
- SHA3-256
- SHA3-384
- SHA3-512
Extendable-output functions (XOFs)
- SHAKE128
- SHAKE256
The higher the size of the message digest, the less the risk of collisions. However, the higher the size the higher the computations. In other words, SHA3-512 is more secure than SHA3-224, but the computations for SHA3-512 requires more time than the computations of SHA3-224.
NIST.FIPS.202 explain in detail how SHA-3 works and the security characteristics.
In general, the basis is to distribute the bits of the input message in a three-dimensional matrix and to perform operations on them. They perform array conversions, bit concatenations, and XORs by blurring the input bits and reducing or increasing their size to the desired length.
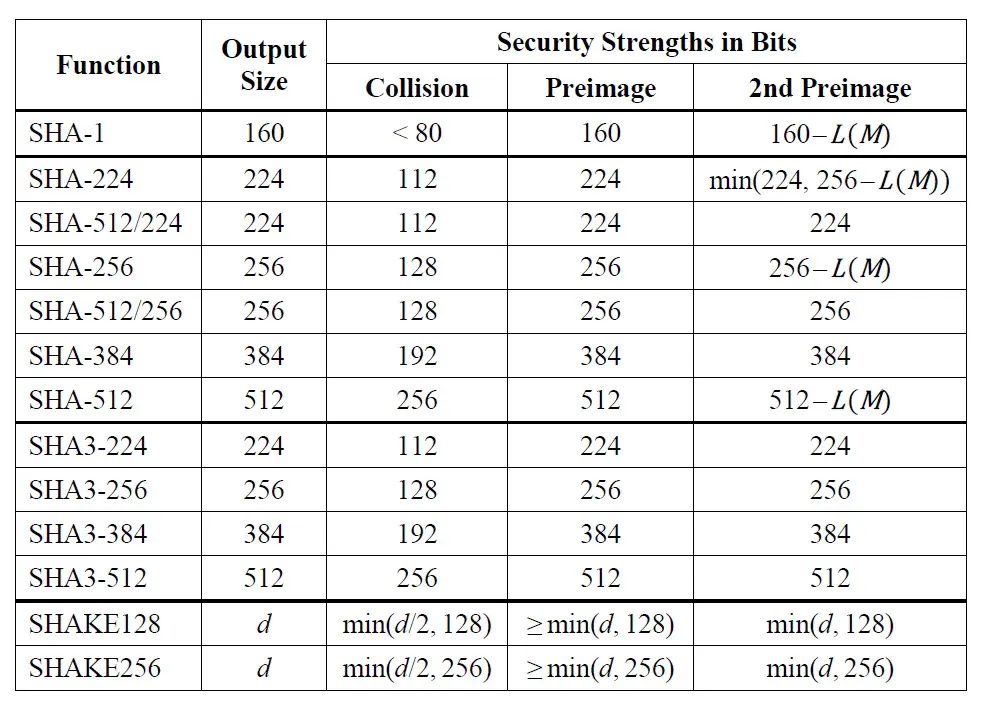
From the table above, you can see that the resistance to collisions of the SHA functions is similar when using equal output lengths. The preimage resistance is equal to the output length of each function and the collision resistance is half that length.
We can see that the greatest advances in SHA-3 are in the resistance to 2nd preimage. That is the resistance to defining another message with the same hash from a message and a known hash.
In this case, the SHA-3 family is superior to its predecessors since when using the same output lengths, it offers the same resistance at the 1st and 2nd preimage. In the SHA-1 and SHA-2 families for some output lengths, the resistance at the 2nd preimage is lower.
SHA is a standard, therefore is used in many areas: software, programming languages and cryptographic applications.
It is usual to find native implementations in programming languages, or as an additional library that can add easily to our projects.
HMAC
Message authentication code (MAC) is the fundamental approach to message authentication. It is a function of the message and a secret key. It will produce a fixed-length value that we can use as an authenticator.
HMAC is a combination of MAC with the result of a cryptographic hash function. It is a way to expand the use of hash functions. Its results depend not only on the message but on a second input that can be a secret key.
You can find a full explanation in RFC 2104.
How HMAC works?
An HMAC function has two inputs: a message and a secret key. We also should know what hash function we are going to use.
After several computations using the message and the secret key, the result is a hash (message digest) that depends on the message and the secret key. To check the authenticity of the message we need the secret key.
HMAC is not an encryption algorithm. Even you have the message digest and the secret key, you cannot obtain the original message.
HMAC usage examples
Find below two examples of how HMAC can be used.
Only authorized users can check the message integrity: If the hash is calculated using an input message and a secret key, only the person with access to the secret key can check the integrity of the message.
Multifactor authentication: Hash functions are used to authenticate users and avoid storing their passwords in plain text. With HMAC, you can store a hash that depends on more than one parameter. For example, the user’s password and a key are calculated from the computer identification. The user’s password is the message, and the computer identification is the password. If we save the HMAC result in a database, during the authentication process the user must enter his/her password and be using an authorized computer to be able to authenticate.
That same process can be done to store the user’s password and the hash resulting from a fingerprint scanner. More than one HMAC can be combined to achieve multi-factor authentication with more than two factors. For instance, an HMAC can be calculated between the text of the message and a secret key. The hash generated by the 1st HMAC can then be fed into a 2nd HMAC and combined with the hash from a fingerprint scanner. In that way, the resulting hash depends on the message, the private key, and a fingerprint scanner. The possibility of combinations depends on the.
HMAC formula
H: Cryptographic hash function
K: secret key
m: message
||: concatenation
+: XOR (exclusive or)
opad: hexadecimal constant
ipad: another hexadecimal constant
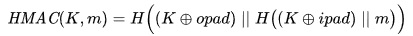
HMAC formula. Source Wikipedia.
See below the order of the operations on the formula for a better understanding.
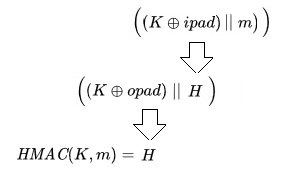
HMAC implementation in Python 3 using SHA-3 hash functions
Find below a python code example of HMAC implementation using SHA-3.
The code is based on the code from Wikipedia, with two differences.
One difference is that sha3_512 instead of MD5.
In the example from wikipedia, if the key-length is less than the block-length it will be fill with 0 and if it is greater then the hash is calculated.
In the example below, we always calculate the hash. That will be the second difference.
from hashlib import sha3_512
#initialize the 2 constants defined in the formula
opad = bytearray((x ^ 0x5c) for x in range(256))
ipad = bytearray((x ^ 0x36) for x in range(256))
blocksize = sha3_512().block_size
#this is the HMAC function
def hmac_sha3_512(key, message):
# calculate the hash of the key, to use a ficed length
key = sha3_512(key).digest()
key = key + bytearray(blocksize - len(key))
t_opad = key.translate(opad)
t_ipad = key.translate(ipad)
# HMAC formula
return sha3_512(t_opad + sha3_512(t_ipad + message).digest())
if __name__ == "__main__":
myHMAC = hmac_sha3_512(b"my secret key ", b"My test message")
print(miHMAC.hexdigest())
HMAC function already implemented in Python
The example from the previous section shows a “manual” implementation of the HMAC function. However, Python has an implementation that we can also use. Always remember one of the principles in programming is code reuse.
Let’s see the example using the implementation that Python 3 provides.
import hmac
from hashlib import sha3_512
if __name__ == "__main__":
myHMAC = hmac.HMAC(b"key", b"message",sha3_512)
print(myHMAC.hexdigest())
H@ppy coding!
Related posts:
