En este artículo se explica el funcionamiento de los algoritmos asimétricos y la firma digital. Entre los algoritmos estudiaremos: Diffie-Hellman, ElGamal y RSA
Los primeros algoritmos de criptografía asimétrica fueron introducidos por Whitfield Diffie y Martin Hellman en la década del 70. Su principal diferencia con respecto a la criptografía clásica y simétrica es que en vez de utilizar una clave para cifrar y descifrar se utiliza un par de claves. Su seguridad se basa de forma general en problemas matemáticos difíciles de resolver.
Aunque los algoritmos asimétricos pueden resultar difíciles de entender debido su base matemática el principio es muy sencillo: Lo que se cifra con una clave se descifra con su pareja. La misma clave no se puede utilizar para cifrar y descifrar el mensaje.
Problema del intercambio de claves
Uno de los principales problemas que tiene la criptografía simétrica cuando se cifra un mensaje es cómo se hace llegar la clave que se utilizó para cifrar al receptor del mensaje. Para ello debe enviarse la clave por una canal de comunicación seguro. ¿Pero si existe ese canal por qué no enviar por ahí mismo el mensaje?
Otra opción es haberse puesto de acuerdo ambos interlocutores previamente. Esa opción muchas veces no es viable. Actualmente se tramita información entre personas que se encuentran muy distantes entre sí y que no tienen la posibilidad de encontrarse personalmente. Imagine que deba visitar cada contacto con quien quiera comunicarse de forma segura utilizando Facebook o WhatsApp. Ese problema al que se enfrentaría se conoce como problema del intercambio de llaves.
Funcionamiento de la criptografía asimétrica o algoritmos asimétricos
En la criptografía asimétrica cada usuario o entidad tiene un par de llaves. Esas llaves son generadas a la vez mediante funciones matemáticas y están estrechamente relacionadas. Pero de una no se debe poder deducir la otra.
Lo que se cifra con una llave se descifra solamente con su pareja. Esa característica de las llaves permite diferentes usos en función de lo que se quiera asegurar en el mensaje. Estos conceptos se explican en el artículo Conceptos generales para estudiar la criptografía.
Algoritmos asimétricos: Cifrado y descifrado de la información
Cada usuario tiene un par de claves. Una es secreta y sola la conoce el usuario. La otra es pública y la conoce todo el que se quiera comunicar con el usuario. Cada algoritmo tiene su forma de implementar este principio pero en conceptos generales funciona como se muestra en el Ejemplo 1:
Ejemplo 1
Usuario A tiene una clave secreta As y una clave pública Ap.
Usuario B tiene una clave secreta Bs y una clave pública Bp.
Se envía un mensaje M desde el usuario A para el usuario B.
El usuario A conoce Bp y cifra el mensaje M con la clave Bp obteniendo el mensaje cifrado Mc.
A envía Mc a B.
Como B tiene Bs descifra Mc con Bs y obtiene M.
Como se puede apreciar cualquier usuario conociendo la clave pública Bp puede cifrar información y enviarla a B. Solo B puede descifrarla porque es quien único conoce su clave secreta Bs.
Lo mismo sucedes si B quiere enviar información a A, debe cifrarla con Ap.
Firma de la información usando algoritmos asimétricos
La firma busca asegurar a B que el mensaje fue enviado por A.
Ejemplo 2
Siguiendo el mismo principio del ejemplo anterior ahora A quiere enviar un mensaje firmado M a B.
Para ello A cifra M con su calve privada As obteniendo Mc.
El mensaje Mc se envía desde A a B.
B utiliza la clave pública Ap para descifrar el mensaje Mc obteniendo M.
Como se puede apreciar cualquiera que conozca Ap puede leer el mensaje, pero solo A pudo haberlo cifrado con As. De esa forma B está seguro que el mensaje es de A.
En el Ejemplo 1 se logra la confidencialidad de la información y en el Ejemplo 2 la autenticidad. Combinando ambos usos de la criptografía es posible que solo B pueda descifrar el mensaje y estar seguro que se lo envió A.
Uso y limitación de los algoritmos asimétricos
El principal inconveniente de los algoritmos asimétricos es que computacionalmente son menos eficientes que los simétricos. Eso quiere decir que son muy lentos para cifrar grandes volúmenes de datos.
Entonces normalmente deben utilizarse en combinación con los algoritmos simétricos y funciones hash para sacarle su máximo provecho cifrando pequeños volúmenes de datos. En el artículo Conceptos generales para estudiar la criptografía se explica en que consisten las funciones hash. Como regla general lo que se firma digitalmente es un hash del mensaje ya que es mucho mas pequeño y al algoritmo le toma menos tiempo.
En el Ejemplo 3 se va a mostrar cómo combinar las familias de algoritmos para lograr diferentes objetivos:
- cifrar los datos con criptografía simétrica
- realizar el intercambio de llaves y la firma del mensaje con criptografía asimétrica
- comprobar la integridad del mensaje con una función hash.
Ejemplo 3
Un usuario A desea cifrar un mensaje M y enviarlo a B.
El usuario A genera una clave privada P. Luego, A cifra M con la clave P utilizando un algoritmo simétrico obteniendo Mp.
La clave privada P se cifra (por el usuario A) con la clave pública Bp utilizando un algoritmo asimétrico obteniendo PBp.
A calcula el hash H1 a M y lo cifra con su clave secreta As utilizando un algoritmo asimétrico obteniendo H1As. Luego de calculado el hash H1 A envía Mp, PBp y HAs a B.
B con su clave privada Bs descifra PBp utilizando un algoritmo asimétrico obteniendo P.
El usuario B descifra Mp utilizando P (y utilizando un algoritmo simétrico) y obtiene M. Luego, B descifra HAs con la clave pública Ap obteniendo H1.
Como siguiente paso, el usuario B calcula el Hash a M obteniendo H2.
Finalmente, B comprueba H1 y H2, si son iguales quiere decir que el mensaje no fue modificado y lo envió A.
Seguridad en los algoritmos asimétricos
La seguridad en los algoritmos asimétricos como se mencionó anteriormente se basa en funciones matemáticas fáciles de ejecutar en un sentido, pero difíciles de ejecutar en sentido inverso.
Cuando se refiere a sentido inverso se está hablando propiamente de las funciones matemáticas. Por ejemplo, la suma y la resta, la multiplicación y la división, la exponenciación y el logaritmo, la derivación y la integración.
Es muy fácil multiplicar o sumar 2 números y obtener un resultado pero es complicado a partir del resultado identificar cuáles fueron los números sumados o multiplicados. El problema se complejiza si el resultado es un numero grande que permite muchas combinaciones.
En el ejemplo 4 se muestra el funcionamiento de un algoritmo de cifrado:
Ejemplo 4
El mensaje es M
La clave secreta es N
El algoritmo de cifrado consiste elevar el número binario que conforma el mensaje al número binario que conforma la clave obteniendo el texto cifrado C.
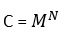
Se envía C como mensaje cifrado.
El criptoanálisis por fuerza bruta para este algoritmo conociendo C consiste en comenzar a probar números N ni M hasta descubrir cuales son los correctos. Lo mismo suceder sin mediante la operación inversa a la exponenciación que es el logaritmo se comienzan a probar números para descubir N y descifrar los mensajes. Recuerde que en los algoritmos asimétricos no se usa la misma clave para cifrar y para descifrar, en este ejemplo la clave de cifrar se obtendría mediante la exponenciación y la de descifrar mediante el logaritmo. Con la capacidad de cálculo actual si se utilizan números primos lo suficientemente grandes probar numeros aletorios hasta dar con el resultado esperado en cualquiera de las 2 operaciones tomaría miles de años.
Números primos grandes
Una forma de facilitar el cálculo es tratar de descomponer los números en números más pequeños y tratar de encontrar el resultado por partes. Por ese motivo las operaciones en criptografía asimétrica tienden a utilizar números primos para que no puedan ser factorizados y los cálculos tengan que realizarse con los números completos. La palabra “grande” se refiere a números con una gran cantidad de dígitos en comparación con la capacidad de calculo existente. En la actualidad se utilizan llaves de 2048 o 4096 bits de longitud.
Tiempo de procesamiento
En la tabla se muestra un ejemplo de la relación de complejidad de algoritmo y tiempo de procesamiento para una capacidad de procesamiento de 1 millón de operaciones por segundo.
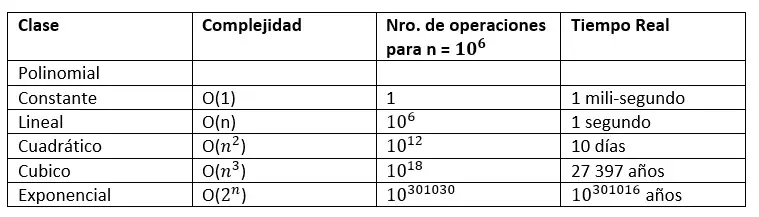
Se puede apreciar que un algoritmo con una complejidad de clase polinomial se calcula prácticamente al instante y de clase exponencial pude tomar millones de años. El objetivo de la criptografía asimétrica es usar funciones matemáticas que para cifrar y descifrar realicen operaciones con una complejidad clase polinomial y su criptoanálisis matemático requiera operaciones de clase exponencial.
La exponenciación es muy utilizada en la criptografía asimétrica porque representa muchas multiplicaciones que a su vez cada una representa muchas sumas y es una operación compleja de realizar. Debido a ello es poco eficiente con grandes volúmenes de datos pero también su repetición continua requiere una gran capacidad de procesamiento.
Basado en lo antes explicado se resume que los algoritmos asimétricos aunque en teoría son matemáticamente criptoanalizables se considera computacionalmente imposible su criptoanalisis en un tiempo aceptable y en eso se basa su seguridad.
Los algoritmos asimétricos deben cumplir con los siguientes requerimientos
Eficiente: Las llaves públicas y privadas deben ser generadas en tiempo polinomial.
Seguro: Con el conocimiento de la llave pública es impracticable obtener la llave secreta.
Condición: Si D es el algoritmo de descifre, E el de cifre entonces, ks la clave secreta, kp la clave pública y Tcl el texto claro se cumple que:
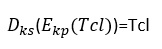
Ahora se va a explicar el funcionamiento de tres algoritmos asimétricos
Algoritmos asimétricos: Diffie Hellman (DH)
Como se mencionó anteriormente Diffie Hellman es el primer protocolo asimétrico de intercambio de claves. Aun se utiliza combinándolo con otros algoritmos añadiéndole fortaleza a su funcionamiento como por ejemplo la firma digital que no se encuentra en el diseño inicial.
El funcionamiento de Diffie Hellman consiste en la aplicación de los siguientes principios matemáticos:
Conociendo que:
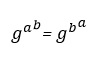
Sustituyendo
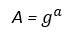
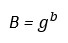
Entonces
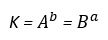
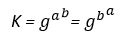
Ahora se mostrará un ejemplo del uso de Diffie y Hellman. Las operaciones matemáticas en el ejemplo se realizan utilizando operaciones modulares (mod. p). En el artículo Entendiendo los principios de la criptografía simétrica a partir del estudio varios métodos de cifrado manual se habla sobre el empleo de las operaciones modulares en la criptografía.
Ejemplo 5:
Los usuarios A y B necesitan compartir una llave K para cifrar sus mensajes. Para la generación de esa llave utilizan el protocolo Diffie Hellman. En las formulas se utiliza “A” y “B” para referirse a dos números calculados. Se utiliza esa notación para facilitar su entendimiento pero no debe confundirse con A y B utilizados para identificar al usuario.
El usuario A calcula un número primo grande “p”
Luego, A escoge 2 números primos aleatorios “g” y “a” y calcula “A”
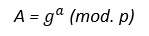
En este momento, A envía “A”, “g”, “p” al Usuario B.
El usuario B escoge 1 número primo aleatorio “b” y calcula “B”
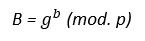
B: envía “B” al Usuario A.
A: calcula la clave secreta K para cifrar el mensaje a partir de la información que le envió B y su clave secreta “a”.
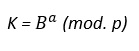
B: calcula la clave secreta K para cifrar el mensaje a partir de la información que le envió A y su clave secreta “b”.
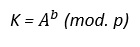
Los usuarios A y B utilizan K que es la misma en ambos extremos como clave secreta para cifrar el mensaje a través de un algoritmo de criptografía simétrica.
Características de seguridad de Diffie Hellman
- Los usuarios A y B tienen un número aleatorio “a” y “b” respectivamente y representan su clave privada.
- Solo A conoce “a” y solo B conoce “b”.
- “a”, “b” y “K” nunca viajan por el canal de comunicación.
- Con la información compartida por el canal tanto A como B pueden generar K.
- Conociendo la información enviada por el canal si no se conoce al menos una de las 2 claves privadas no es posible generar K.
Algoritmo ELGAMAL
Fue inicialmente diseñado para producir firmas digitales y posteriormente también se utiliza para cifrar mensajes.
Generación de llaves
- Escoger un numero primo grande “n”.
- Seleccionar dos números primos aleatorios “p” y “x” menores que “n”.
- Se calcula “y”.
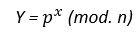
La llave secreta es: “x”.
La llave pública es: “Y”, “p” y “n”.
Firma digital
Para firmar un mensaje “m” se siguen los siguientes pasos:
- Se escoge un numero aleatorio “k” que sea primo relativo con (“n”-1) y se calcula “a” y “b”.
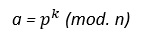
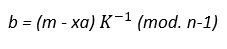
La firma consiste en el par “a”, “b”. Debe mantenerse en secreto “k” y utilizar uno diferente cada vez.
Comprobar la firma digital
Para el receptor comprobar que la firma digital del mensaje “m” es válida debe cumplirse la siguiente condición:
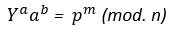
Si se cumple, la firma es verdadera y el mensaje no fue modificado, si no se cumple el mensaje es falso.
Cifrar
- Se escoge primero un número aleatorio k primo relativo con (n-1), que será mantenido en secreto y se calculan “a” y “b”.
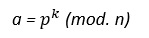
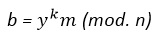
El par “a”, “b” es el texto cifrado.
Descifrar
Para descifrar se realiza la siguiente operación:
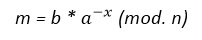
Algoritmo RSA
Debe su nombre a sus tres inventores: Ronald Rivest, Adi Shamir y Leonard Adleman.
Sus llaves sirven indistintamente tanto para cifrar como para firmar.
Generación de llaves
- Seleccionar aleatoriamente dos números primos grandes, “p” y “q”.
- Calcular el producto “n” = pq.
- Escoger un número “e” primo relativo con (p – 1)(q – 1).
- “e” debe tener inversa módulo (p – 1)(q – 1), por lo que existirá un número “d” tal que:
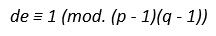
Llave secreta: “d”.
Llave pública: “e”, “n”.
Cifrado
Se cifra con la clave pública del destino.
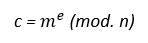
Descifrado
El destino lo descifra con su clave privada.
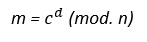
Firma
El origen cifra el mensaje con su clave privada
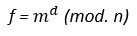
Comprobación
El destino descifra el mensaje con la clave pública del emisor. Si se obtiene el mensaje quiere decir que solo el emisor pudo haberlo firmado.
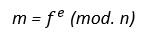
Conclusiones sobre los algoritmos asimétricos
- De los tres algoritmos estudiados probablemente el más fácil de implementar y entender es el RSA, por eso es uno de los mas utilizados.
- El protocolo DH es utilizado principalmente para crear claves de sección para proteger conexiones. Con el mismo se puede generar una clave de un solo uso para cada conexión y se desecha una vez se desconectan ambos extremos.
- Los algoritmos asimétricos se basan en la seguridad computacional que ofrece realizar operaciones con complejidad polinomial y que requieren un criptoanálisis con complejidad exponencial.
- El texto cifrado o firmado con ELGAMAL está compuesto por un par de números, mientras que con RSA solamente por uno.
- Los algoritmos asimétricos son eficientes cifrando pequeños volúmenes de datos, por lo cual generalmente se utilizan para el intercambio de claves y la firma digital.
