Funciones Hash criptográficas y HMAC

En el presente artículo se describen las características que debe cumplir una función hash criptográfica y los usos que se le puede dar. Además, se analizan las propiedades de algunas funciones hash existentes. Finalmente, se explica en qué consiste HMAC y se muestra un ejemplo de su implementación.

Función hash

Es una función de una unidireccional que transforma un mensaje M en un mensaje de con longitud predefinida. Unidireccional se refiere a que es fácil de calcular en un sentido pero difícil o imposible en sentido inverso.

Las funciones hash también son conocidas como función resumen o función picadillo. El resumen o hash no debe interpretarse con un resumen del contenido del texto. El hash genera una secuencia de bits a partir de un texto de entrada pero no brinda información sobre su contenido.

Un mismo mensaje de entrada al aplicarle la misma función hash siempre genera la misma salida. El hash no es un algoritmo de cifrado ya que su funcionamiento no debe permitir a partir del hash obtener el texto que lo generó, o lo que en un algoritmo de cifrado seria descifrar el mensaje.

Función hash criptográfica

Las funciones hash se agrupan en 2 grandes familias, las funciones hash criptográficas y las no criptográficas. Aunque ambas familias cumplen con la condición de generar un resumen a partir de un mensaje, las criptograficas deben cumplir con una serie de requisitos adicionales de seguridad.

• Resistencia a preimagen: La preimagen de un hash es el mensaje o los mensajes que pueden generar ese hash. La resistencia a preimagen consiste en que a partir del hash debe ser computacionalmente imposible obtener el mensaje que lo generó. Esa característica es muy importante cuando se desea garantizar la confidencialidad del mensaje, por ejemplo cuando se trabaja con contraseñas.

• Compresión: El hash va a tener una longitud fija sin importar la longitud del mensaje que lo origina. Generalmente el hash es más pequeño que el mensaje que lo genera.

• Facilidad de cálculo: El hash debe rápido de calcular por las computadoras modernas.

• Difusión: El hash del mensaje debe generarse a partir de una función compleja o varias funciones simples que dependan de la totalidad de los bits del mensaje. Si se modifica un solo bit en el mensaje de entrada debe variar al menos la mitad de los bits en el hash resultante.

• Resistencia a 2da preimagen: Conociendo el hash y una preimagen no debe ser posible encontrar una 2da preimagen que genere el mismo hash. Esa característica también se conoce como resistencia a colisiones simples.

• Resistencia fuerte a colisiones: No debe ser posible crear dos mensajes o preimágenes que generen el mismo hash.

Es importante señalar que el hash tiene una longitud fija y que los mensajes de entrada tienen una longitud variable y generalmente son más largos que el hash. Eso quiere decir que hay mayor cantidad de mensajes de entradas que posibles hash y por lo tanto en algún momento dos mensajes de entrada van a coincidir en un hash.

En teoría no se elimina el riesgo de colisiones ya que la longitud máxima de entrada es mayor que la de salida. Lo que debe ser computacionalmente impracticable es encontrar de forma intencional dos mensajes con la misma salida. Los requisitos de seguridad de las funciones hash criptográficas giran en función de no dar información del mensaje y que no sea posible encontrar otro mensaje que genere el mismo hash.

Usos de las funciones hash

Las funciones hash tienen varios usos atendiendo a las características antes descritas. Algunos son:

• Almacenar contraseñas: Es una buena práctica no guardar en bases de datos las contraseñas en texto claro. Si una contraseña es almacenada en texto claro en una base de datos y alguien logra acceder a la misma entonces obtendría las credenciales de autenticación de los usuarios. En su lugar se almacena un hash de la clave del usuario. Cuando el usuario escribe su clave en el sistema informático este calcula el hash y comprueba con la base de datos. Si el hash coincide con el hash de la base de datos entonces la contraseña es correcta. Mediante este procedimiento el sistema nunca almacena la contraseña del usuario y es posible comprobar si es correcta en el momento que la escribe.

• Firma digital: El proceso de la firma digital requiere operaciones matemáticas complejas. Por su complejidad firmar un mensaje grande resulta poco eficiente y toma bastante tiempo. En su lugar, se calcula un hash al mensaje. Debido a que el hash tiene una longitud fija generalmente es mucho más pequeño que el mensaje original. Se firma digitalmente el hash del mensaje. Como el hash solo pudo ser generado por ese mensaje, por transitividad firmar su hash equivale a firmar el mensaje. Cualquier modificación en el mensaje original va a provocar que el hash no coincida con el hash firmado. En el artículo “Funcionamiento de los algoritmos asimétricos y la firma digital” explica la firma digital.

• Comprobar integridad: Una forma de comprobar la integridad de un fichero es publicar el hash del fichero. Cuando alguien descarga el fichero para estar seguro que no fue modificado o que no se ha descargado incorrectamente puede calcular el hash al fichero descargado. Luego compara ese hash con el publicado y si es el mismo el fichero es correcto.

• Comprobar contraseña antes de descifrar: Cuando se está diseñando un cifrado o algún sistema para cifrar se puede almacenar el hash de la clave que se utilizó para cifrar el contenido como parte del fichero cifrado. Cuando el usuario escribe la clave esta se comprueba con el hash para detectar si es correcta antes de comenzar a descifrar y no intentar descifrar los datos con una clave incorrecta.

Familia de funciones hash SHA-3

Actualmente entre las funciones hash criptográficas se considera seguro utilizar la familia de los SHA “Secure Hash Algorithm”.SHA-3 es la 3ra generación de la familia precedida por SHA-1 y SHA-2. Cada una agrupa un conjunto de funciones hash en diferentes versiones.

SHA-3 agrupa 6 funciones publicadas como estándar por el Instituto Nacional de Normas y Tecnología (NIST) de los Estados Unidos. Sus características están publicadas en el NIST.FIPS.202. Las 6 funciones están integradas por 4 funciones hash y 2 funciones de salida extensible (XOF). Las funciones de salida extensible permiten generar un hash de cualquier longitud y es posible adaptarlo a requerimientos de tamaño diferentes a los definidos en las funciones hash.

El número final de la función hash representa la longitud de la salida, por ejemplo SHA3-256 representa la función SHA3 con una salida de 256 bits. En el caso de las funciones de salida extensible el número representa el nivel de seguridad de esa salida extensible.

Funciones hash de SHA-3

• SHA3-224
• SHA3-256
• SHA3-384
• SHA3-512

Funciones XOF de SHS-3

• SHAKE128
• SHAKE256

Las funciones hash al generar una salida más grande tiene menos riesgo de colisiones pero también requiere más procesamiento. Por lo tanto se considera más seguro usar SHA3-512 que SHA3-224 pero su cálculo consume más tiempo.

En el NIST.FIPS.202 se explica detalladamente el funcionamiento y características de seguridad de SHA-3. De forma general se basan en distribuir los bits del mensaje de entrada en una matriz tridimensional y realizar operaciones sobre los mimos. Realizan conversiones de matrices, concatenaciones de bits y XOR difuminando los bits de entrada y reduciendo o aumentando su tamaño hasta llegar a la longitud deseada.

En la Ilustración 1 tomada del NIST.FIPS.202 se muestra la seguridad de las familias SHA-1, SHA-2 y SHA-3 frente a colisiones, resistencia a 1ra preimagen y 2da preimagen.

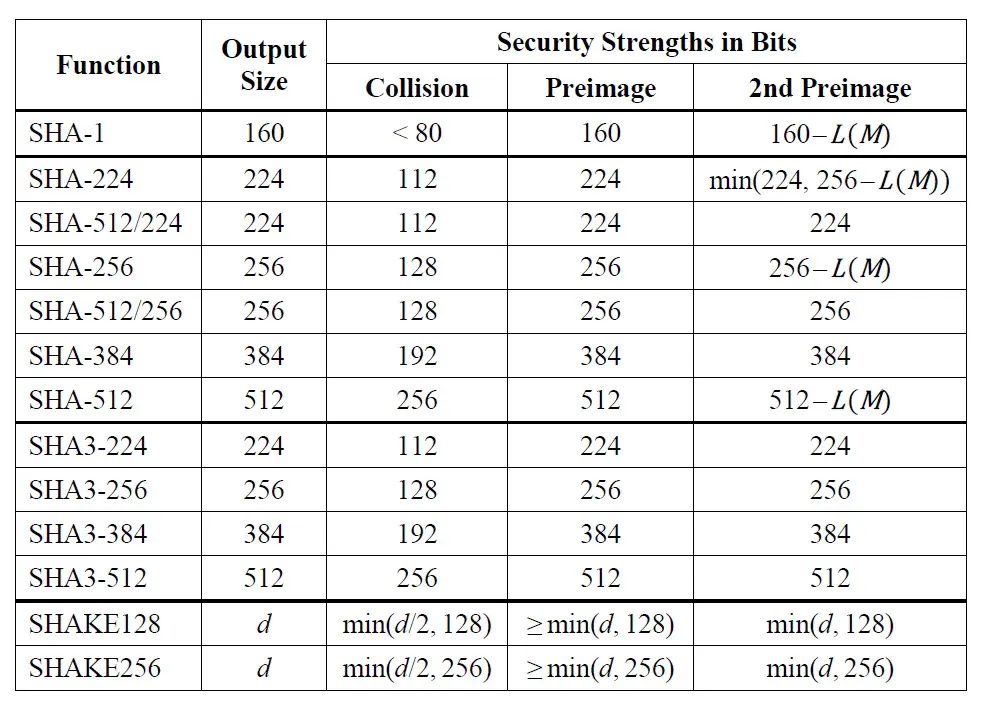
Analizando la tabla se puede apreciar que la resistencia a colisiones las 3 familias es similar en longitudes de salida iguales. La resistencia a preimagen es igual a la longitud de salida de cada función y la resistencia a colisiones es la mitad de dicha longitud.

Los mayores avances de SHA-3 se aprecian en la resistencia a 2da preimagen, es decir, la resistencia a que partir de un mensaje y un hash conocido se pueda definir otro mensaje con el mismo hash. En ese caso la familia SHA-3 es superior a sus predecesoras ya que en iguales longitudes de salida ofrece la misma resistencia a 1ra y 2da preimagen. En las familias SHA-1 y SHA-2 en algunas longitudes de salida la resistencia a 2da preimagen es inferior.

SHA al ser un estándar es soportado por la mayoría del software, lenguajes de programación y aplicaciones criptográficas. Cuando no viene incluida nativa-mente en el sistema lo más probable es que haya una biblioteca compatible que la implemente.

HMAC

La función HMAC o “hash con clave” combina el “message authentication code” (MAC) con el resultado de una función hash. Es una forma de ampliar el uso de las funciones hash ya que el resultado no depende solo del hash del mensaje sino de otro parámetro que puede ser la clave secreta del usuario. La definición y explicación del HMAC esta descrita en el RFC 2104.

Funcionamiento de HMAC

La función HMAC tiene como parámetros de entrada el mensaje y la clave secreta. Debe estar definida la función hash que se va a utilizar. En principio se puede utilizar cualquier función hash que sea compatible con la longitud del mensaje de entrada.

Luego se realizan operaciones entre el mensaje y la clave y se le calcula el hash en más de una ocasión. El resultado es un hash que depende del mensaje y la clave. Para poder comprobar la autenticidad del mensaje también es necesaria la clave.

El HMAC no es un algoritmo de cifrado ya que, aunque se tengo el hash resultante y la clave no se puede obtener el mensaje original.

Ejemplos de uso de HMAC

• Solo los autorizados pueden comprobar la integridad del mensaje: Si el hash se calcula a partir del texto del mensaje y una clave secreta, solo quien tenga la clave secreta puede comprobar la integridad del mensaje.

• Autenticación multifactor: Como se explicó anteriormente las funciones hash se utilizan para la autenticación de los usuarios y evitar almacenar en texto claro sus contraseñas. Con HMAC se puede almacenar un hash que dependa de más de un parámetro. Por ejemplo, la contraseña del usuario y una clave calculada a partir de la identificación de la computadora. La clave del usuario es el mensaje y la identificación de la computadora es la clave. Si el resultado del HMAC se guarda en la base de datos, luego durante el proceso de autenticación el usuario tiene que escribir su contraseña y estar trabajando en la PC autorizada para poder autenticarse. Ese mismo proceso se puede realizar para almacenar la contraseña del usuario y el hash del resultado de un escáner de huella dactilar por poner otro ejemplo.

Se puede combinar mas de un HMAC para lograr un autenticación multifactor con más de dos factores. Por ejemplo se puede calcular un HMAC entre el texto del mensaje y una clave secreta. Luego el hash generado por el 1er HMAC puede introducirse a un 2do HMAC y combinarlo con el hash de un escáner de retina. De esa forma el hash resultante depende del mensaje, la clave privada y un escáner de retina. La posibilidad de combinaciones depende de las necesidades de quien lo necesite a utilizar.

Fórmula del HMAC

H: función hash criptográfica

K: clave secreta

m: mensaje

||: concatenación

+: el símbolo similar al signo de suma representa XOR.

opad: constante exadecimal para relleno.

ipad: otra constante exadecimal para relleno.

( ): Los paréntesis se utilizan para definir el orden de las operaciones de forma similar a las fórmulas matemáticas.

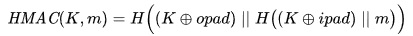
Ilustración 2: formula de HMAC copiada de la Wikipedia.

Un desglose de la fórmula para facilitar su compresión

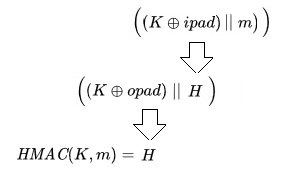
Ejemplo de implementación manual de HMAC en Python 3

A continuación se muestra un ejemplo de implementación de HMAC utilizando la función SHA-3 en python. El código similar al que se encuentra publicado en la Wikipedia con 2 modificaciones. La 1ra es que se utiliza la función sha3_512 en lugar de MD5. La segunda es que en el de la Wikipedia si la clave es menor que la longitud del bloque se rellena con 0 y si es mayor se calcula el hash. En el ejemplo presentado en cualquier caso se calcula el hash.

#!/usr/bin/env python
#importar las funcion sha3_512, tambien pueden ser sha3_224, sha3_256, sha3_384 etc...
from hashlib import sha3_512

#crear las 2 constantes definidas en la documentacion
opad = bytearray((x ^ 0x5c) for x in range(256))
ipad = bytearray((x ^ 0x36) for x in range(256))
blocksize = sha3_512().block_size 

#definir el nombre de la funcion
def hmac_sha3_512(clave, mensaje):
#    calcular el has a la clave para trabajar con una longitud fija
    clave = sha3_512(clave).digest()
    
    clave = clave + bytearray(blocksize - len(clave))
    t_opad = clave.translate(opad)
    t_ipad = clave.translate(ipad)
    #sustituir la formula de HMAC con funciones de pyton
    return sha3_512(t_opad + sha3_512(t_ipad + mensaje).digest())
    #la funcion digest retorna un binario

if __name__ == "__main__":
    #  llamo la funcion con una clave y un texto de prueba    
    miHMAC = hmac_sha3_512(b"mi clave secreta", b"este es un mensaje de prueba")
    print(miHMAC.hexdigest())
    #la funcion hexdigest transforma el binario en exadecimal para mostrarlo en la consola

Uso de la función HMAC de Python

El ejemplo anterior fue una implementación manual de HMAC pero si está programando lo más lógico es utilizar la implementación que trae el propio lenguaje de programación. Ocupa menos espacio en el código y lo más probable es que funcione de forma más eficiente.

A continuación se muestra un ejemplo utilizando la función HMAC que tiene integrada Python a partir de la versión 3.0.

#!/usr/bin/env python

#importo las funciones sha3_512 y hmac
import hmac
from hashlib import sha3_512

if __name__ == "__main__":
    
   #ejecutar la funcion hmac con parametros "clave", "mensaje", "funcion hash"
    miHMAC = hmac.HMAC(b"mi clave", b"este es otro mensaje de prueba",sha3_512)
    print(miHMAC.hexdigest()) #mostrar el resultado en la consola