Just Cryptography

Learn Cryptography and Information Security

Home » Blog » How to generate RSA key pairs

How to generate RSA key pairs

The Rivest-Shamir-Adleman (RSA) scheme is the most widely accepted approach for public-key cryptography. Here I’ll show you how to generate RSA key pairs.

The RSA algorithm to generate the key pairs is as follows:

  1. Choose p, q, two prime numbers
  2. Calculate n = pq
  3. Calculate f(n) = (p-1)(q-1)
  4. Chose e such that gcd(f(n), e) = 1; 1 < e < f (n), and
  5. Chose d, such that ed mod f(n) = 1

After these calculations, the private key is {d,n} and the public key is {e,n}. The numbers p, q, and d must be kept private.

Example of key pair generation using the RSA algorithm

Let’s see the following example with specific numbers so you get a better idea.

  1. p=17 and q =11. Notice 17 and 11 are both prime numbers
  2. n= 11 x 17 = 187
  3. f(n) = (17-1)(11-1)=160
  4. e=7, notice that gcd(160,7)=1 and 1<7<160
  5. d=23, notice that (7 x 23) mod 160 =1. You can calculate d using the extended Euclid’s algorithm.

The private key is {23,187} and the public key is {7,187}

Remember, the numbers 17, 11, and 23 (p, q, and d) must be kept private.

Key considerations

The protection against a brute force attack for RSA is the same as many other ciphers: to have a big keyspace. The bigger d is in bits, the better. Just also consider that the bigger the keys the slower the encryption and decryption process. The recommended key size for RSA is 2048.

For a longer explanation of key size, you can read this post.

Several RSA codes have been broken so far, up to 678 bits in 2010. Therefore, in real-life applications, we cannot choose p and q as in the example before. At least if we want to keep our secrets.

What to do now?

The recommendation is to use RSA 2048-bit as a minimum. For this, we don’t have to do the process manually. Several software applications will do it for us.

Let’s see how it works in some of them.

RSA key pair generation in Python

Find below the code of a Python example to generate the RSA keys using the module Cryptography.

from cryptography.hazmat.primitives.asymmetric import rsa
from cryptography.hazmat.primitives import serialization
private_key = rsa.generate_private_key(
     public_exponent=65537,
     key_size=2048,
)
private_bytes = private_key.private_bytes(
    encoding=serialization.Encoding.PEM,
    format=serialization.PrivateFormat.TraditionalOpenSSL,
    encryption_algorithm=serialization.BestAvailableEncryption(b'mypassword')
)
print (private_bytes)
public_key = private_key.public_key()
public_bytes = private_key.public_key().public_bytes(
    encoding=serialization.Encoding.PEM,
    format=serialization.PublicFormat.SubjectPublicKeyInfo
)
print (public_bytes)

RSA key pair applications

The RSA algorithm is widely used. It is implemented as part of many tools that we use daily, even though sometimes we don’t know we are using it.

See the three examples below.

SSL and HTTPS

Most of the time you are using a web browser, you are using HTTPS. This is a secure protocol because all the communication is encrypted. It is basically “the old” HTTP over SSL.

If you can see a padlock in the web URL from your browser, you are using HTTPS.

Padlock next to the URL indicating the use of HTTPS protocol

It is basically the use of a digital certificate, which communicates the public key of the server to the client.

Some of these certificates use RSA, as you can see in the picture below.

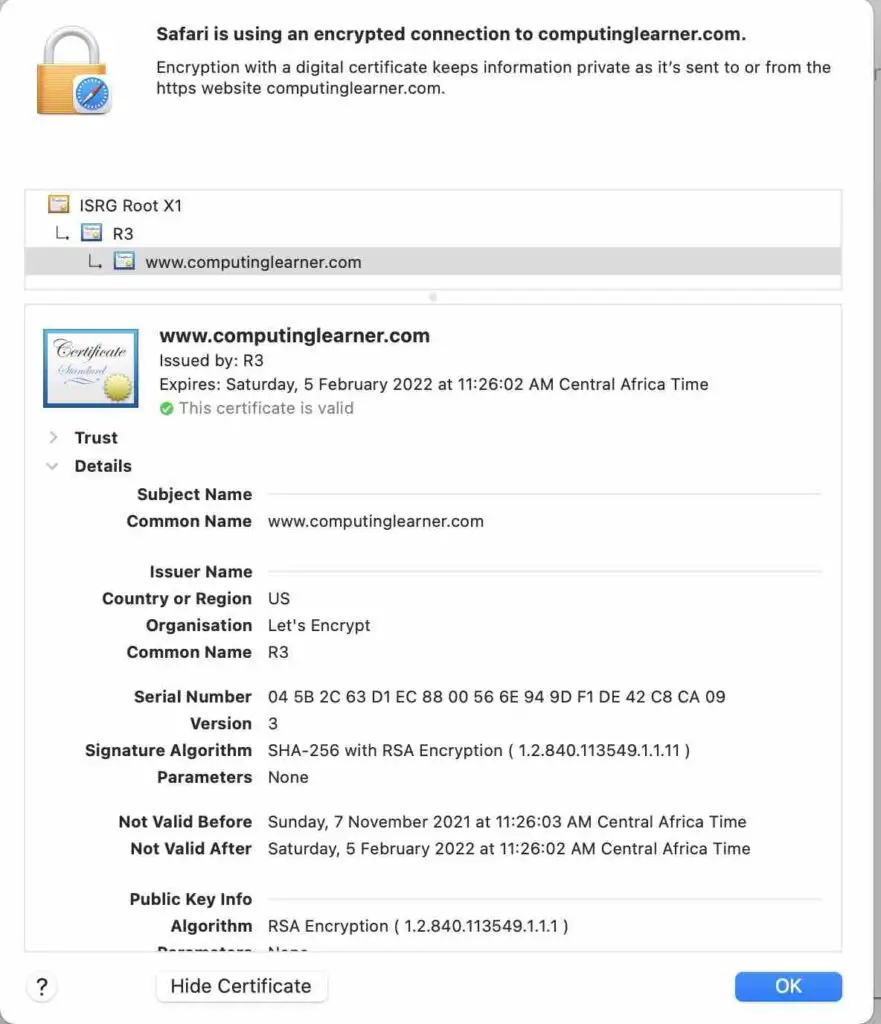
Sample of usage of RSA in a Public key Certificate
Sample of usage of RSA in a Public key Certificate

See an example of how to create an SSL certificate, which includes an RSA key pair in this link.

Public Key Certificates

A Public Key Certificate, also known as a Digital certificate, is a way of sharing your public key without the use of intermediaries. It is very useful, and it is widely used in web servers. Notice that even you don’t need an intermediary to share your public key, you do need the intermediary to verify the certificate.

See a full explanation of what a digital certificate is in this post.

Digital Signatures

The RSA algorithm can also be used for digital signatures.

In this case, the sender will create a hash of the message/document, then encrypt the hash with the private key.

The receiver gets a plain message/document with a signed hash. Then, will decrypt the hash with the sender’s public key. After that, the receiver creates a hash of the plain message/document and will compare it with the decrypted one. If they are the same, the signature is valid.

SSH

“ Secure Shell (SSH) is a cryptographic network protocol for operating network services securely over an unsecured network. Typical applications include remote command-line, login, and remote command execution, but any network service can be secured with SSH.” Source Wikipedia.

This service uses RSA to encrypt the communication and keep it secure.

See below for an example of how the RSA key pair can be generated.

ssh-keygen -t rsa

When you execute the command above, you will be asked for a passphrase. After that, two files will be generated, one with the private key and one with the public key.

It is recommended to use a passphrase, so your private key is encrypted on your hard drive. In case someone can steal your file, you won’t be able to see your plain text private key.

Summary

The recommended length of RSA keys is a minimum of 2048-bit.

RSA is widely used, some examples are SSL, HTTPS, Digital certificates, and Digital Signature.

Because the key must be big enough to avoid the code to be broken, the encryption process is slow. Therefore, its use is not recommended to encrypt big amounts of data. In the case of digital signature, this is done by encrypting a hash of the message instead of the message itself.

Related posts

,

Recent posts