SHA-2 is a family of cryptographic hash algorithms used to create message digest to verify the integrity of information (usually files). They are the current standard in cryptographic hash functions and have several applications, included digital signatures.
Table of Contents
- Introduction
- SHA-2
- SHA-2 General Scheme
- General scheme of the SHA-2 functions
- SHA-256 function
- SHA-512 function
- SHA-1 and SHA-2 characteristics summary
- SHA-2 in python
- SHA-2 message digest from the command line
Introduction
SHA-2 is based on the Merkle-Damgård construction. Find below an illustration of this construction.
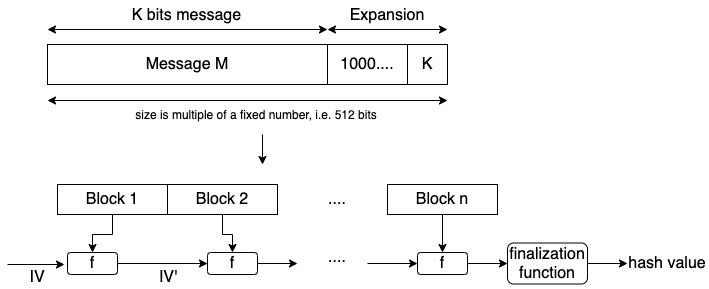
Notice that the original message is processed in blocks. The blocks are concatenated using an initial vector (IV) and a function f. The value of the initial vector will change with each concatenation and at the end, we obtain the hash value.
The size of the message digest will vary according to the SHA-2 function you use. At the end of this article, I’ll show you a summary table with the output size of each function.
SHA-2
With SHA-2 we can create message digests of 224, 256, 384, and 512 bits.
SHA-224 is the result of SHA-256 truncated to the right-most 224 bits.
SHA-384 is the result of SHA-512 truncated to the right-most 384 bits.
There are other two variants of SHA-512:
- SHA512/224 uses words of 32 bits instead of 64 bits.
- SHA512/384 uses words of 64 bits.
The SHA-512 based variants are more resistant to length extension attacks, therefore they are more recommended than the other variants.
SHA-2 General Scheme
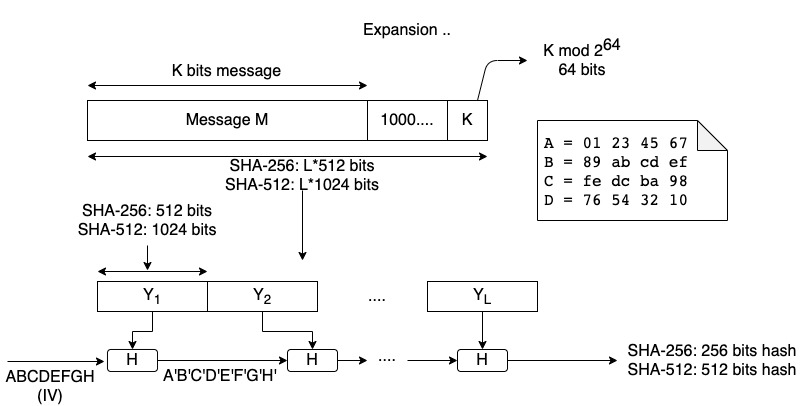
In the figure above we can see the general scheme of the SHA-2 family.
The general overview is as follows:
- It expands the message as MD5 and SHA-1 as all of them follow the Merkle-Damgård construction.
- SHA-256 process the message using 512-bits blocks
- SHA-512 uses 1024-bits blocks
- The Initial Vector has 8 words. SHA-256 uses 32-bit words and SHA-512 uses 64-bit words.
- The size of the digest is 8×32=256 for SHA-256 and 8×64=512 bits for SHA-512.
Let’s examine the algorithm that processes each block.
General scheme of the SHA-2 functions
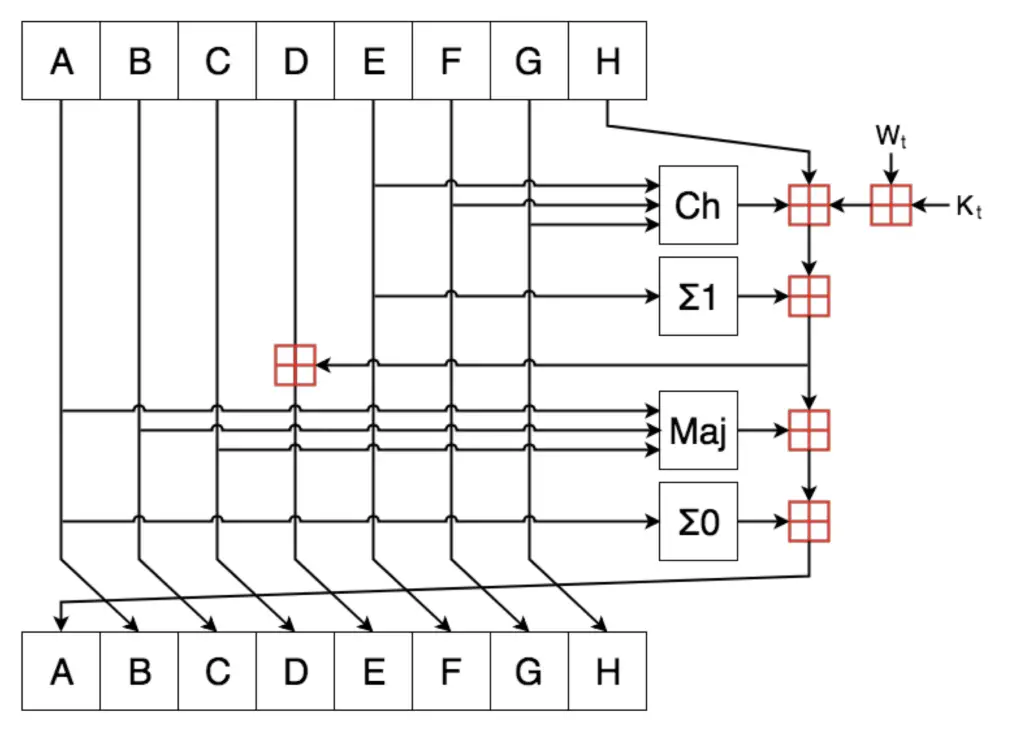
The words A, B, C, D, E, F, G, and H are created by taking the 32 bits for SHA-256 and 65-bits for SHA-256 of the decimal portion of the square root of the first 8 prime numbers. You don’t need to calculate them yourself. Those numbers are public and if you want to implement the algorithm you can define them as constants.
Ch and Maj are logical operations.
Ch ( E , F , G ) = ( E AND F ) XOR ( NOT E AND G )
Maj ( A , B , C ) = ( A AND B ) XOR ( A AND C ) XOR ( B AND C )
Σ0 and Σ1 are XOR operations repeated over the same word from the initial vector and they will depend on whether we are using SHA-256 or SHA-512.
As with the previous MD5 and SHA-1, at the end of each operation, the Initial Vector values are shifted as shown in the above figure.
SHA-256 function
Initial Vector values (32 bits of the decimal portion of the square root of the first 8 prime numbers):
- A = 6a09e667
- B = bb67ae85
- C = 3c6ef372
- D = a54ff53a
- E = 510e527f
- F = 9b05688c
- G = 1f83d9ab
- H = 5be0cd19
In this case, we have to extend the words from 16 to 64. The first 16 words are obtained from the 512-bits block. The rest are created using XOR operations, rotations, and shifts using the words we already have.
Kt is a 32-bits constant, created from the first 64 prime numbers.
Ch and Maj are defined in the previous section.
Σ0 and Σ1 are XOR and shift operations over the same word (from the Initial Vector). In this case, they are defined as:
- Σ0 ( A ) = ( A ⋙ 2 ) XOR ( A ⋙ 13 ) XOR ( A ⋙ 22 )
- Σ1 ( E ) = ( E ⋙ 6 ) XOR ( E ⋙ 11 ) XOR ( E ⋙ 25 )
SHA-512 function
Initial Vector values (64 bits of the decimal portion of the square root of the first 8 prime numbers):
- A = 6a09e667f3bcc908
- D = a54ff53a5f1d36f1
- G = 1f83d9abfb41bd6b
- B = bb67ae8584caa73b
- C = 3c6ef372fe94f82b
- E = 510e527fade682d1
- F = 9b05688c2b3e6c1f
- H = 5be0cd19137e2179
In this case, we have to extend the words from 16 to 80. The first 16 words (of 64-bits each) are obtained from the 1024-bits block. The rest are created using COR operations, rotations, and shifts using the words we already have.
Kt is a 32-bits constant, created from the first 80 prime numbers.
Ch and Maj are defined in the previous section.
Σ0 and Σ1 are XOR and shift operations over the same word (from the Initial Vector). In this case, they are defined as:
- Σ0 ( A ) = ( A ⋙ 28 ) XOR ( A ⋙ 34 ) XOR ( A ⋙ 39 )
- Σ1 ( E ) = ( E ⋙ 14 ) XOR ( E ⋙ 18 ) XOR ( E ⋙ 41 )
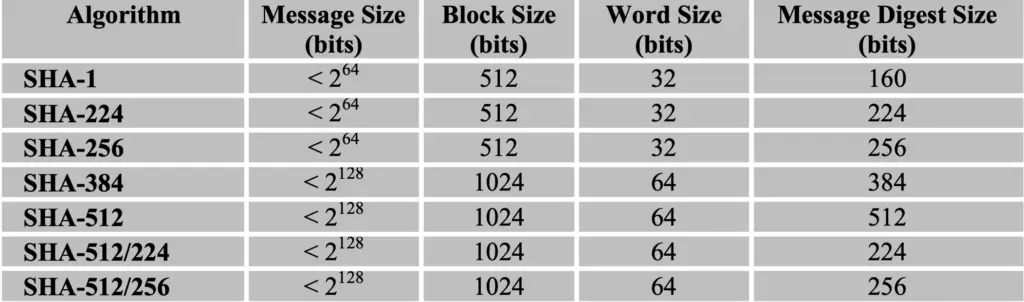
SHA-1 and SHA-2 characteristics summary
SHA-2 in python
import hashlib
print('SHA-512')
message_digest = hashlib.sha256(b'This is my message')
print(message_digest.hexdigest())
message_digest = hashlib.sha256(b'This is my message.')
print(message_digest.hexdigest())
print('SHA-512')
message_digest = hashlib.sha512(b'This is my message')
print( message_digest.hexdigest())
message_digest = hashlib.sha512(b'This is my message.')
print(message_digest.hexdigest())After executing the previous code, we can get the following result.
rafel@Rafaels-iMac crytography % python3 sha-2.py
SHA-512
3311b7c0bd91b6c73a38212de8ade31c51910f17480ad212ed2b9798a35b7747
fc8a08660bbc44f56d2c06220919ee063d3eb90e708dd68fa248f0cae53ea91d
SHA-512
11fe4123cf5b956e0fa2c2574dc023ff9ff197132c265e5e0a88c17a198a20669e722a7f842644ff7b47ce892719b18b076344554151d919d069c259af0399bc
dd97c16fdcc9d4ae3d690e54a28a301c2efaec558cdd232325cae8448809c2d181b0c0a0ed11868026bbebc2b47a69ec9cd5386eba42f3797222ed6378a01c79
rafel@Rafaels-iMac crytography % SHA-2 message digest from the command line
We can execute this command from the console on MacOS. Notice that we have to specify the function after the ‘-a’ option.
rafel@Rafaels-iMac ~ % echo -n This is my message | shasum -a 256
3311b7c0bd91b6c73a38212de8ade31c51910f17480ad212ed2b9798a35b7747 -
rafel@Rafaels-iMac ~ % echo -n This is my message | shasum -a 512
11fe4123cf5b956e0fa2c2574dc023ff9ff197132c265e5e0a88c17a198a20669e722a7f842644ff7b47ce892719b18b076344554151d919d069c259af0399bc -
rafel@Rafaels-iMac ~ % It is similar to Linux based system; you just use the command line sha256sum. You can also use the app openssl that is available in Linux and other operating systems.
Related posts:

