Elliptic Curve Cryptography (ECC) is a modern Public Key Cryptosystem. ECC is difficult to explain because of all the mathematics background you need to understand the algorithms. In this post, I’ll give you a practical approach and I’ll show you how you can generate key pairs using ECC and Python.
Example of key pair generation using the ECC algorithm
The private key in ECC is just a random integer. So, you can use any random number generator (that is cryptographically strong) and generate a number big enough.
In the case of the public key, it is a point (x and y coordinates) over a certain ECC curve. See in the section below the ECC curves approved by NIST.
Approved ECC curves by NIST
See below a table that shows the NIST-approved ECC curves and the security strength that can be achieved in each case.
| ECC Curve | Targeted security strength |
| secp224r1 | s=112 |
| sect233k1 | 111<s<129 |
| sect233r1 | 111<s<129 |
| sect283r1 | 111<s<129 |
| secp256r1 | 111<s<129 |
| sect283k1 | 111<s<129 |
| secp384r1 | 111<s<193 |
| sect409k1 | 111<s<129 |
| sect409r1 | 111<s<129 |
| secp521r1 | 111<s<257 |
| sect571k1 | 111<s<257 |
| sect571r1 | 111<s<257 |
Notice that different curves will have different levels of security. One reason why the popularity of ECC is increasing is that it can achieve similar security strength than RSA with a smaller key size.
For example, for RSA to achieve a 256-bit security strength, it needs a 15360-bit key, while ECC needs a 512-bit key. For more information about the different key sizes needed for a specific security strength, you can click on this link.
Key considerations
The protection against a brute force attack for ECC is the same as other ciphers: to have a big keyspace. The bigger the key is in bits, the better. Just also consider that the bigger the keys the slower the encryption and decryption process. The recommended key size for ECC is 256.
For a longer explanation of key size, you can read this post.
Let’s see how to generate the key pair in Python.
ECC key pair generation in Python
You can use the Python code below to generate the ECC keys using the module tinyec.
Notice that this module is fully implemented in Python. Therefore, there are no dependencies. Also, it is not suitable for production environments. You should only use it to get a better understanding of the algorithms and how they work.
from tinyec import registry
import secrets
ecc_curve = registry.get_curve('secp224r1')
private_key = secrets.randbelow(ecc_curve.field.n)
public_key = private_key * ecc_curve.g
print("private key:", private_key)
print("public key:", public_key)After running the code above, you can get an output similar to this one.

Remember the private key is a random integer, so you won’t see the same keys if you execute the code on your computer, or even if you execute it twice on the same computer.
Notice that in this case, we are using the ECC curve ‘secp224r1’. There are other ECC curves that you can use with the library tinyec. Feel free to explore.
ECC key pair applications
ECC can be used for the same applications as the rest of public-key algorithms:
- Encryption/Decryption
- Digital signatures
- Key exchange
You can also see ECC applications in digital certificates (key exchange) in your browser. See an example below on how ECC is used in SSL certificates.
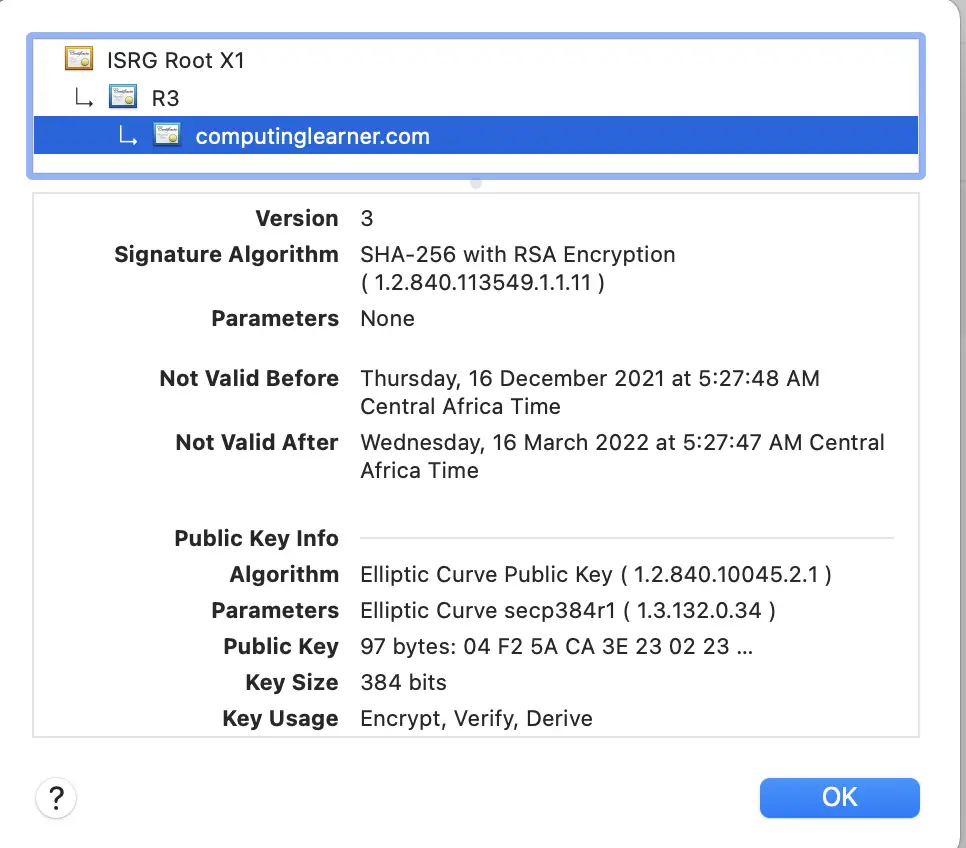
Notice that this certificate is using a 384-bit key, by using the elliptic curve secp384r1.
Summary
ECC curves are attractive to use because they can achieve the same security strength as other standards like RSA but use a smaller key size. As a result, the operations with ECC curves are more efficient.
There are several NIST-approved curves, each of which provides different security strengths.
Related posts
