Asymmetric Cryptography: The RSA algorithm (with examples)

The Rivest-Shamir-Adleman (RSA) algorithm is the most widely accepted approach in asymmetric cryptography. Asymmetric cryptography means that one key is used to encrypt and a different, but related one is used to decrypting the message.

The RSA algorithm is as follows:

Choose p, q, two prime numbers
Calculate n = pq
Calculate f(n) = (p-1)(q-1)
Chose e such that gcd(f(n), e) = 1; 1 < e < f (n), and
Chose d, such that ed mod f(n) = 1
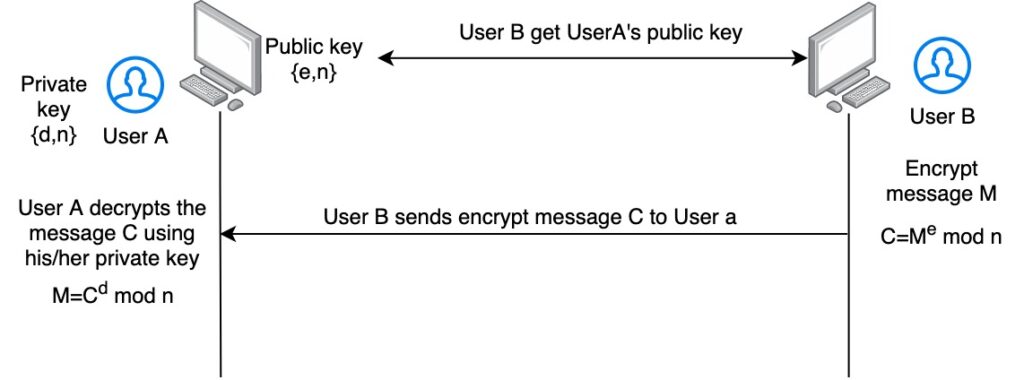
The private key is {d,n} and the public key is {e,n}
To encrypt a message M you use the formula C = M^e mod n, where {e,n} is the public key of the receiver you want to send the message.
To decrypt the message C, the receiver uses the formula M = C^d mod n, where {d,n} is the private key of the receiver.

Notice that from steps 1 to 6, you are just calculating the private and public keys. This is something that perhaps you won’t do it too much. In other words, once you generate a key pair, you can use it for a certain amount of time.

Steps 7 and 8, are the ones used anytime you want to send a message to someone, first to encrypt and then to decrypt the message on the receiver side. See below a graphical description of how it works.

Let’s see an example below.

Example 1

First, let’s assume you calculated your keys as follows:

p=17 and q =7. Notice 17 and 7 are both prime numbers
n= 17 x 7 = 119
f(n) = (17-1)(7-1)=96
e=11, notice that gcd(96,11)=1 and 1<11<96
d=35

The keys are:

private key: {35,119}
public key: {11,119}

Now, you published somehow your public key and I want to send you a message only you can read.

The message I want to send you is M=21. Notice that you can always find a numeric representation for any message. At the end of the day, all data in a computer is represented as numbers.

C = M^e mod n=21¹¹ mod 119 = 98

When you receive the encrypted message C=45, you use your private key to decrypt it.

M = C^d mod n=98³⁵ mod 119 = 21

Example 2

I wrote a whole post to explain how the RSA key-pair is created (steps 1-6). If you want to get a better understanding and see how these numbers are calculated, including a python implementation, you can find it here.

Let’s say you calculated your private and public keys. The next step is to make your public key available so if someone wants to send you a message, it can use it. You can read about one of the mechanisms for public key distribution here.

These are your keys:

private key {23,187} (d,n)
public key is {7,187} (e,n)

I decided to send you a message and I don’t want anyone else, but you, to be able to read the message.

The message I want to send you is represented by the number 99. Notice that you can convert your text into numbers, just by using ASCCI code or the binary representation of the message you want to send.

I now proceed to encrypt the message M=99

C = M^e mod n=99⁷ mod 187 = 176

Now, I can send you the encrypted message C=176 over an insecure network. If someone intercepts the message, he/she won’t be able to know that I sent you the message M=99.

Once you received the message, you proceed to decrypt it.

M = C^d mod n=176²³ mod 187 = 99

Because only you know your private key {d,n}, only you will be able to decrypt the message. Actually, this will be true only if the sizes of the keys you choose are big enough. The strength of this algorithm relies on the size of the keys used. To learn more about why the size of the key matters you can read this post.

One of the RSA applications is in Public Key Certificates, also known as Digital Certificates. You can read about one of the applications of RSA in this post.

Asymmetric Cryptography: The RSA algorithm (with examples)

Example 1

Example 2

Recent posts